Performance Characterization of Cooperative Localization and SLAM

  • Motivation
    • The goal of this project is to provide theoretical tools for characterizing the accuracy of robot localization. In particular, our work focuses on three classes of localization problems:

    1. Cooperative Localization (CL)
    2. Simultaneous Localization and Mapping (SLAM)
    3. Cooperative SLAM (C-SLAM)

    Mobile robot teams have attracted the interest of the robotics community, because of the increased efficiency and reliability resulting when multiple robots cooperate for performing a task. In particular, localization (CL, SLAM, and C-SLAM) has been the most active research area of mobile robotics for the past two decades. This is due to the fact that it permits accurate pose estimation in unknown environments necessary for autonomy.
    However, most of the research work on CL, SLAM, and C-SLAM has focused on implementation techniques and on addressing the problem of computational complexity. The issue of analytical evaluation of performance has been largely ignored in the literature, with only few exceptions of limited scope. As a result, questions such as "How much more accurate will the position estimates become if the odometry noise variance is reduced by 50%?", or "Will a particular set of sensors allow a robot to achieve localization errors smaller than 1m after 1h of operation?" can only be answered after extensive simulations and/or time-consuming experimentation. Clearly, this is a significant obstacle for efficient robot design. Our work aims at providing analytical means for answering such questions.
  • Contribution
    • The primary contribution of this work is the derivation of theoretical tools for evaluating the performance, in terms of positioning accuracy, of CL, SLAM, and C-SLAM. In particular, we present analytical expressions that determine the guaranteed accuracy of localization, as a function of the following system-design parameters:
    • the accuracy of the robots' sensors
    • the number of robots and features
    • the structure of Relative Position Measurement Graph (RPMG) that describes the measurement topology between the robots and/or landmarks
    • the statistical properties of the robots' trajectories
    • the spatial distribution of features, in SLAM and C-SLAM
    These expressions predict the localization accuracy a given robot design and facilitate the process of selecting the appropriate sensors for meeting the accuracy requirements of a given task. Moreover, the availability of analytical results enable one to study the properties of positioning errors during CL, SLAM, and C-SLAM and develop an intuitive understanding of the interaction between the system parameters. This knowledge will lead to design rules, which will reduce the time and effort required for new robot designs. Prior to this work, experimentation and numerical simulations were the only tools available for studying the trade-offs between selections of such parameters. These time-consuming methods become necessary only after a design has been finalized merely for validation purposes.
  • Approach
    • Our specific goal is to study the properties of the state covariance matrix during pose estimation, since this matrix is a concrete measure of the uncertainty. The main challenge with this problem is that the models describing both the motion and the measurements of robots moving in 2D and 3D are generally nonlinear. As a result, the Extended Kalman Filter (EKF), rather than the linear Kalman filter, is applied for state estimation, and the Riccati recursion, which describes the time evolution of the covariance, is time-varying. For this Riccati no closed-form solution exists in the general case.
    Therefore, in order to analytically study the properties of CL for robots moving in 2D, we resort to the derivation of upper bounds for the covariance of the position estimates. In particular, in our work we derive upper bounds on
    • the worst-case uncertainty of the position estimates, and
    • the expected uncertainty of the position estimates
    Email Updates: In the latter case, prior information about the statistical properties of the robot's trajectories (and of the features' distribution, in the case of SLAM), is utilized.
    In order to compute the upper bounds on the worst-case uncertainty, our approach is based on deriving a "bounding" LTI system, whose covariance at every time step is provably an upper bound of the covariance in the original, nonlinear system. This is achieved by determining upper bounds on the system noise covariance matrix and the relative position measurement covariance matrix. By obtaining the steady-state solution of the Riccati corresponding to this LTI system, we are able to predict the guaranteed asymptotic accuracy of localization. A similar approach, based on defining a different "bounding" LTI system, whose covariance is provably an upper bound to the expected uncertainty of the original nonlinear system, is followed for characterizing the expected performance of the system.
  • Results
    • The performance of this algorithm has been demonstrated in both in real-world experiments, and in extensive simulation tests. We here describe the results of: (i) a large-scale experiment in an uncontrolled urban environment, and (ii) an experiment in a typical office environment.
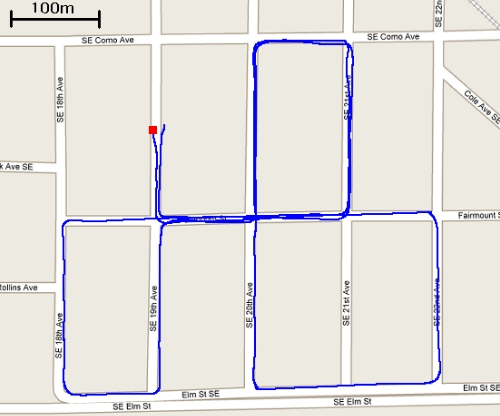
    For the outdoor experiment an IMU/camera sensor payload was mounted on top of a car moving in a residential area of Minneapolis. The car traveled a total distance of approximately 3.2 km, over a time period of 9 min. The camera used for this experiment is an IEEE 1394 camera, recording images of resolution 640 x 480 pixels at a rate of 3 Hz, while the IMU is an Inertial Science ISIS IMU, recording inertial measurements at 100 Hz.
    Some example images from the recorded dataset are displayed below:
    As shown in the above example images, several moving objects appear in the image sequence, and moreover, the leaves of the trees move due to the wind. Despite these challenging conditions, the filter was able to successfully and accurately track the position, velocity, and attitude of the vehicle. The estimated trajectory, superimposed on a satellite map of the area, is shown below:
    In addition to the satellite map, we also superimpose the estimated trajectory on a street map:
    Even though ground truth for the entire trajectory is not available, from the above plots we can conclude that the estimated trajectory closely follows the street layout. The final position error is known, and it is approximately 10 m (i.e., approx. 0.3% of the traveled distance). This excellent position accuracy is achieved without loop closing, and without using prior information about the motion (for example, nonholonomic constraints or a street map). It is also worth noting that even though images were only recorded at 3Hz due to limited hard disk space on the test system, the estimation algorithm is able to process the dataset at 14Hz, on a single core of an Intel T7200 processor (2GHz clock rate). During the experiment, a total of 142903 features were successfully tracked and used for EKF updates.
    In addition to the above outdoor experiment, we have also tested the algorithm's performance in an indoors experiment. In this case, the IMU/camera system moves in a typical office setting (the main MARS lab office). Some example images from the sequence are the following:
    Note that for this experiment we have used a wide-angle lens, which creates the black areas at the periphery of the images. Here is a snapshot of the 3D trajectory estimate:
    The trajectory in this case is approximately 84m long, while the final error is less than 40cm (i.e. error less than 0.5% of the traveled distance).
  • Videos


    • >
  • Relevant Publications
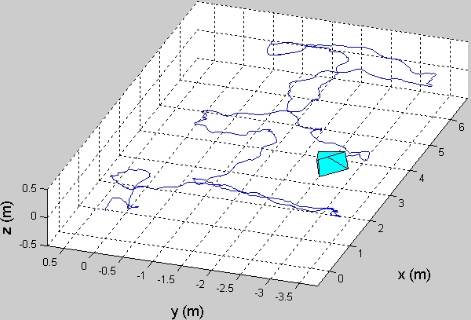
  • C1. A.I. Mourikis, S.I. Roumeliotis: "A Multi-state Constraint Kalman Filter for Vision-Aided Inertial Navigation," In Proceedings of the IEEE International Conference on Robotics and Automation, April 10-14 2007, Rome, Italy,  pp. 3565-3572.
  • Acknowledgements
    • This work was supported by the University of Minnesota (DTC), the NASA Mars Technology Program (MTP-1263201), and the National Science Foundation (EIA-0324864, IIS-0643680).