Performance Characterization of Cooperative Localization and Tracking

  • Summary

    • The idea of employing sensor networks for target tracking has recently become attractive, as the result of advances in the manufacturing of low-cost communication and sensing devices. When multiple nodes of a sensor network measure the distance and bearing to a target of interest, the acquired data can be processed (either at a central fusion center or in a distributed fashion) in order to estimate the target's position. When instead of static, mobile sensors are employed, a larger area can be covered without the need to increase the number of nodes in the sensing network. Moreover, the configuration of the sensors can be changed so as to adapt to the motion of the target. For example, a team of robots can actively pursue a target to prevent the target's escape from the visibility range of sensors.
    When a team of robots is employed for tracking a number of targets, the position of the robots (Localization) and the position of the targets (Tracking) need to be concurrently estimated. In this project we study the problem of Cooperative Localization and Target Tracking in scenarios where teams of, possibly heterogeneous, mobile robots track the position of multiple targets. Specifically, we develop the analytical tools required for performance characterization of these systems.
    Performance characterization is the most important step that must be taken before any investment in system development is made. We must be able to predict the robots' performance on average and in the worst case before actually implementing the system. Here, performance refers to the accuracy of position estimation and is assessed by the state estimates' covariance for the robots and the targets. In particular we are interested in an analysis of the positioning performance in terms of the number of robots and targets, sensors' characteristics, and the structure of Relative Position Measurement Graph (RPMG) that describes the measurement topology between the robots and the targets.
    In this project, by employing an Extended Kalman Filter framework, we develop a set of worst-case bounds for the positioning accuracy of the robots and the targets. Furthermore, we investigate how a priori information about the stochastic distribution of the robots' and targets' position can be utilized to derive bounds for expected value of the position estimate covariance. This performance analysis is based on:
    1. The derivation of a "bounding" Linear Time Invariant (LTI) system whose covariance at every time step is provably greater or equal to that of the original non-linear system. This is achieved by determining upper bounds on the system noise covariance matrix and the relative position measurement covariance matrix.
    2. The solution of the Riccati equation for the LTI system.
    The resulting expressions for the upper bound on the localization and tracking covariance are closed-form expressions of key parameters of the system such as the number of robots and targets, the accuracy of the robots' odometric and tracking sensors, the structure of the RPMG, and the dimensions of the area within which the tracking task takes place.
    These performance bounds can be employed in order to predict the positioning accuracy in a certain tracking application, and thus can facilitate the task of sensor selection so as to meet user-imposed requirements.
  • Experimental Results
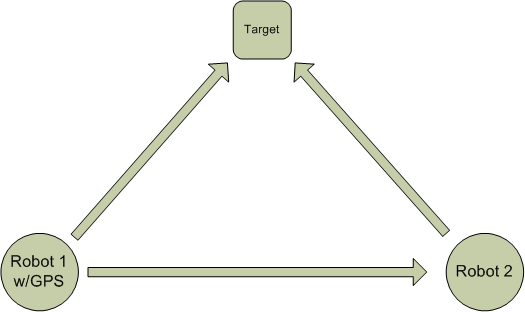
    • We have carried out experiments to verify our theoretical analysis. The RPMG for the experiment shown here is shown in the following figure:
    Figure 2: Target's (dashed black line) and robots' (solid red and blue lines) trajectories. The blue dots denote the return points of a laser scan taken during the experiment (they are included to facilitate visualization of the area where tracking took place).
    Figure 3: Actual covariance (solid lines) and covariance bounds (predicted by the closed-form expressions - dashed lines) for the robots and the target.
  • Simulation Results
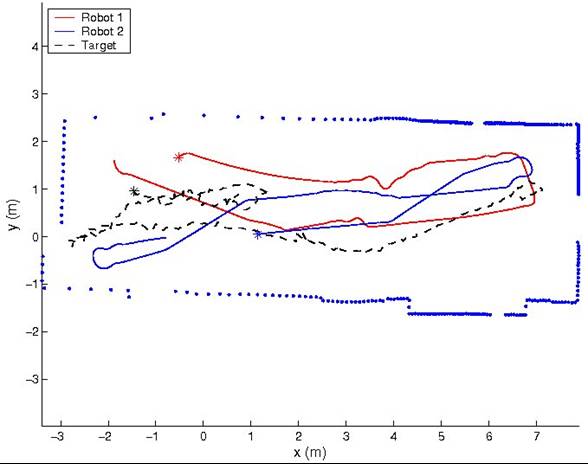
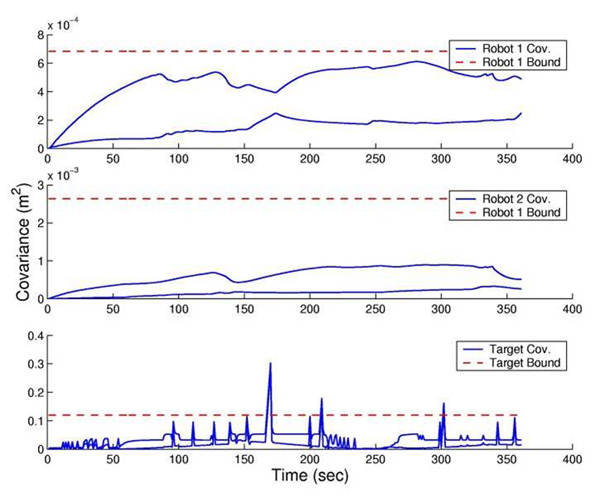
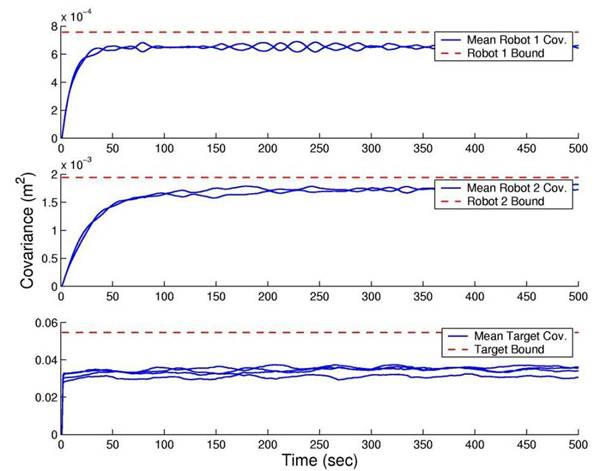
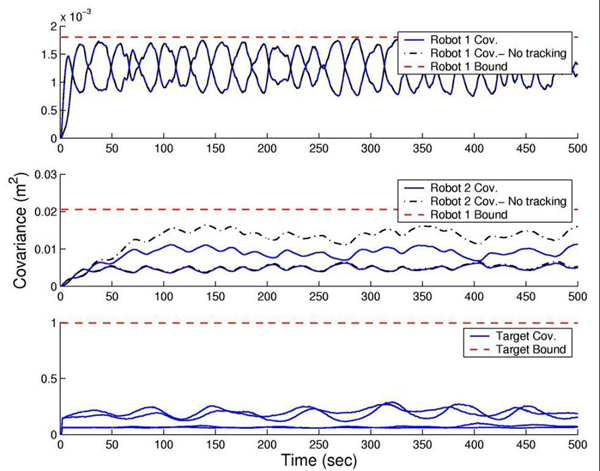
    • To test the bounds on the expected uncertainty, extensive simulation tests have been carried out. The results are shown in the following figures:
    Figure 1: Actual covariance (averaged - solid blue lines) and expected covariance (predicted - dashed red lines) for the robots and the target.
    Figure 2: Top two subplots: predicted covariance bound (red dashed lines), robot covariance when targets are detected but without any knowledge about their motion model - i.e., infinite target propagation noise covariance (solid black lines), robot covariance when the targets are ignored - i.e., the robots perform cooperative localization (dashed black lines). Third subplot: predicted covariance bound (dashed red line) and actual covariance (solid blue lines) for the target.
  • Extensions
    • We are currently extending the results of this work to the cases where both robots and targets navigate in 3D. Additionally, we are planning to address the problem when distance-only or bearing-only measurements are used for tracking the targets.
  • Relevant Publications
  • C1. F.M. Mirzaei, A.I. Mourikis, and S.I. Roumeliotis, "On the Performance of Multi-robot Target Tracking", In Proc. 2007 IEEE International Conference on Robotics and Automation (ICRA'07), Rome, Italy, Apr. 10-14, pp. 3482-3489 (pdf).