Determining the Robot-to-Robot Relative Pose using Range-only Measurements
- NSF
-
Tasks that involve multiple robots require knowledge of their relative position and orientation (i.e., coordinate transformation). Before a group of robots can cooperate, each of them needs to know where the others are and where they are heading to. With this information, the robots can perform tasks such as collision avoidance, cooperative localization and mapping, and formation control. When both robot-to-robot relative distance and bearing measurements are available, determining their coordinate transformation is straightforward. However, due to limitations of the equipment used and/or constraints of the environment operating in, in many cases only distance measurements are available (i.e., range sensors are cheap and widely available and they are often directly embedded in wireless communication devices).
In this work, we address the problem of determining the relative pose of pairs robots that move on a plane while measuring the distance to each other as shown in the figure below. We have proved that the minimum number of distance measurements required for computing the 3 degrees of freedom relative pose is 3. In this case, we have shown that there exist at most 6 solutions. In order to disambiguate them, additional distance measurements are necessary. We have further shown that given 4 distance measurements there exist at most 4 solutions. Finally, we have proved that 5 distance measurements are sufficient for uniquely determining the vehicles' relative pose.
Our main contributions are: (i) we provide all algebraic solutions in closed form when given 3, 4, or 5 distance measurements, and (ii) we present a fast linear algorithm for determining the unique solution when given 5 distance measurements. Furthermore, with additional distance measurements, we use the solution of our linear algorithm as initial point and apply an iterative weight Least Squares algorithm to refine our initial estimate. This way, we account for the effect of measurement noise and get better estimates in fewer iteration steps (i.e., increase robustness and speed of convergence of the iterative process).
Two robots' trajectories: The odd (even) numbered frames of reference depict the consecutive poses of robot 1 (robot 2). dij denotes the distance between the two robots when aligned to frames {i} and {j} respectively.
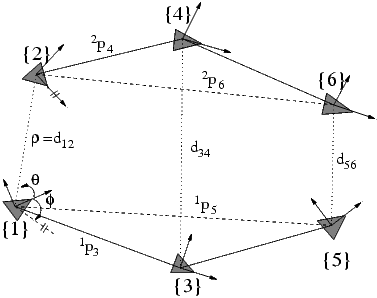
6 Real possible relative transformations given the same set of measurements:
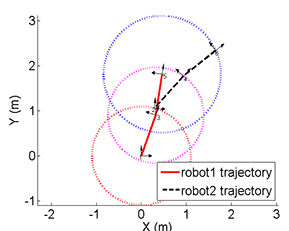
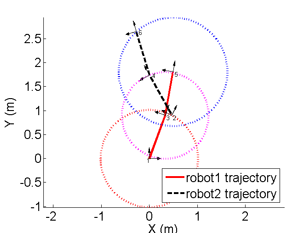
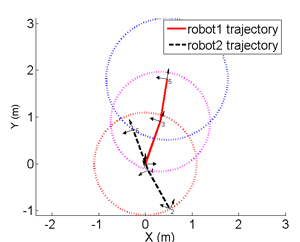
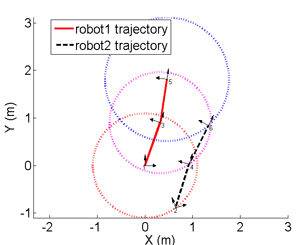
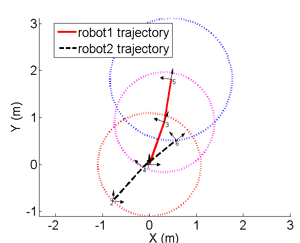
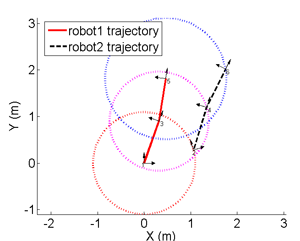
The unique solution given 5 distance measurements:
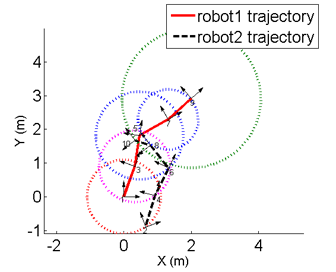
- C1. X. S. Zhou and S. I. Roumeliotis, "Determining the Robot-to-Robot Relative Pose Using Range-only Measurements," in Proceedings of IEEE International Conference on Robotics and Automation, Rome, Italy, April. 10 - 14 2007. pp. 4025-4031 (pdf).